
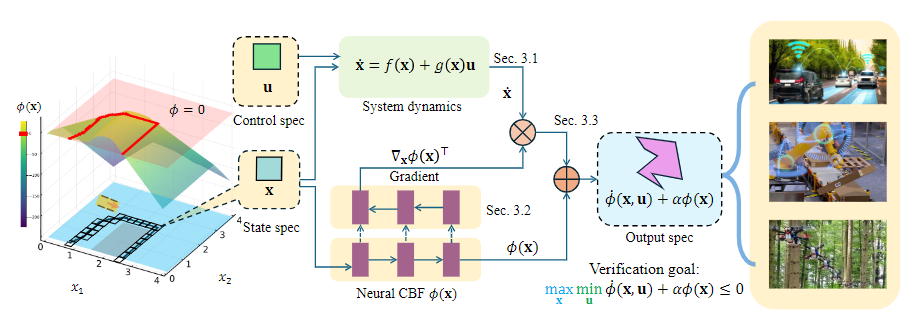
Ensuring safety in control systems, especially those involving robots, is paramount. Control Barrier Functions (CBFs) have emerged as a powerful tool for guaranteeing safety constraints. Recently, neural networks have been used to parameterize CBFs, offering the advantage of handling complex systems. However, verifying the correctness of these neural CBFs is a significant challenge. This post dives into a groundbreaking research paper that tackles this problem head-on, presenting a novel verification framework that's significantly faster and more reliable than existing methods.
Traditional methods for verifying CBFs often struggle with the complexity of neural networks. Their non-linearity and lack of explicit mathematical interpretability make it difficult to definitively prove that a neural CBF will always maintain safety constraints across all possible system states and inputs. Existing techniques, such as interval bound propagation, often lead to overly conservative bounds, resulting in many false negatives (failing to verify a correct CBF).
The research paper, "Verification of Neural Control Barrier Functions with Symbolic Derivative Bounds Propagation," introduces a novel solution. Instead of relying on interval arithmetic, it leverages symbolic derivative bound propagation. This clever technique combines:
This approach leads to significantly tighter bounds compared to existing methods, resulting in higher verification rates and faster computation times.
The researchers tested their method on various robot dynamics (Dubins car, point robot, planar quadrotor) with varying neural network complexities. The results are impressive: their method achieved a 20% higher verified rate with reduced verification time compared to state-of-the-art baselines (NNCB-IBP and BBV). Heatmaps and tables vividly illustrate the superiority of this new approach.
While impressive, the method does have limitations. Scalability remains a concern, as computational cost can still increase significantly with higher-dimensional state spaces and more complex networks. Additionally, the reliance on ReLU activation functions and approximations in the system dynamics and optimal control inputs could lead to false negatives or less tight bounds. Future research could focus on extending this method to other activation functions, refining approximation techniques, and integrating verification directly into the neural CBF training process.
This research presents a significant advance in verifying neural CBFs. The proposed symbolic derivative bound propagation method offers a substantial improvement in efficiency and effectiveness, paving the way for more reliable and safer autonomous systems. The higher verification rates and faster computation times are compelling evidence of its potential to transform safety-critical control system design.